Weighing Different Deal-Making Methods at a Final Table

I was playing on the final table at a recent Las Vegas tournament when someone asked "Should we chop?" The question led to a heated discussion.
The small stack said "only if it's an equal chop." The large stack said "only if it's a chip-chop." I said "only if it's an ICM chop." Further discussion made it clear: many players don't really know the differences between these different methods of chopping the final table prize pool.
Chopping Variants
There are three basic ways to chop a tournament prize pool:
- ICM Chop - prizes are awarded according to the Independent Chip Model
- Equal Chop - everyone gets the same prize
- Chip-Chop - each player gets a prize proportional to the size of his stack via one of two methods: (1) prizes are proportional to the chips each player has, or (2) the next prize is awarded to everyone, then the remaining money is awarded proportionally according to the chips each player has
Clearly these chop methods do not create the same prize distribution.
The Independent Chip Model
The Independent Chip Model was originally developed as a "fair" method to estimate the value of our tournament stack in a chop situation. For example, an ICM chop might be used at the final table of a multi-table tournament or among the last few players in a sit-n-go.
Bill Chen points out in The Mathematics of Poker that "there is no easy answer to the question of mapping chip stacks to prize equity, even for players of equal skill." Nevertheless, several models have been developed to do just that, the most common being the Malmuth-Harville model.
This is not a simple model. It iteratively tries to determine the chances that a particular player will finish in each position. This gets more and more complex as the number of players increases, which has led some researchers to create other models which purport to be "more accurate."
Reasonable models can produce somewhat different ICM equities, but ultimately, these modest differences are swamped by the reality of how a tourney actually plays out. Nevertheless, for the purpose of chopping up a remaining prize pool, Malmuth-Harville is just fine.
ICM Calculators
Luckily, we don't need to understand the math ourselves. We can use one of several free online calculators. There are also several phone apps that allow us to run a chop calculation at the table.
One calculator I like is from ICMIZER, available here. It can model up to 15 players with an easy-to-use interface. Below, Figure 1 shows an example of a final table chop with five remaining players as calculated by the ICMIZER.
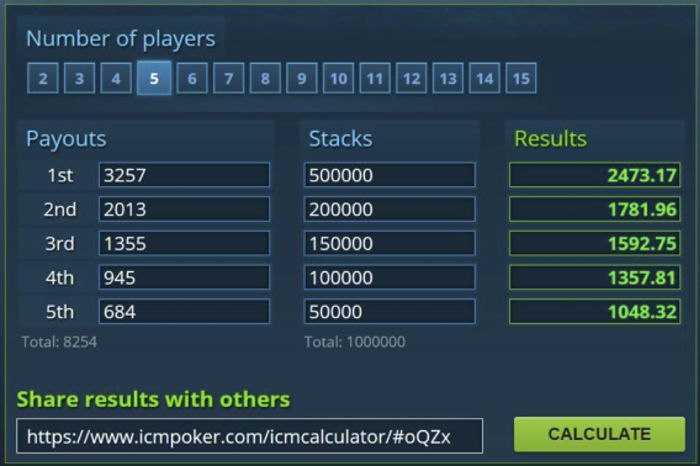
A more powerful calculator can be found at HoldemResources, available here. This one allows up to 256 players, so we can model the impact of ICM on more than simple chopping situations. Figure 2 shows the output for the same final table chop as Figure 1 as found with the HoldemResources calculator. Notice that the results are the same.
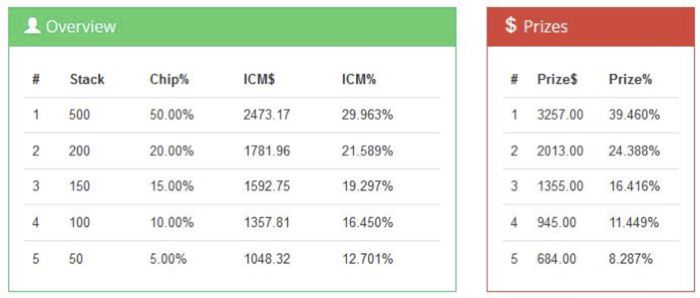
Chop Example
Suppose we are five-handed in a $150 MTT with 100 entrants. The total prize pool was $11,200 and the remaining prize pool is $8,254. The remaining prizes and stack sizes are summarized in Figures 1, 2 and 3.
| Prizes | Place | Stack | Chip% | ICM% | ICM$ Chop | Equal Chop | C-Chop #1 | C-Chop #2 |
|---|---|---|---|---|---|---|---|---|
| $3,257 | 1 | 500,000 | 50% | 30.0% | $2,473 | $1,651 | $4,127 | $3,101 |
| $2,013 | 2 | 200,000 | 20% | 21.6% | $1,782 | $1,651 | $1,651 | $1,651 |
| $1,355 | 3 | 150,000 | 15% | 19.3% | $1,593 | $1,651 | $1,238 | $1,409 |
| $945 | 4 | 100,000 | 10% | 16.5% | $1,358 | $1,651 | $825 | $1,167 |
| $684 | 5 | 50,000 | 5% | 12.7% | $1,048 | $1,651 | $413 | $926 |
We can see that Player 1 has 50 percent of the total chips in play, but ICM awards him only 30 percent of the remaining prize pool, which is $2,473. Let's compare this to the other chopping methods.
An equal chop is very unfair to the chip leader, reducing his prize to only $1,651. But a chip-chop would be unfair to the other players. Indeed, chip-chop method #1 would award him $870 more than first-place money! Even chip-chop method #2 awards him nearly the full first-place prize.
We can also see that the small stack has only 5 percent of the total chips. ICM awards her 12.7 percent of the remaining prize pool or $1,048, which is slightly better than fourth-place money. But an equal chop awards her a much larger prize, better than third-place money. On the other hand, chip-chop method #1 awards her less than the fifth-place award! How fair is that?
Caveats
The Independent Chip Model is not without its drawbacks.
- ICM assumes that the tourney ends immediately. That's fine for a chop, but it's a big assumption when we use it for in-tourney strategy decisions.
- ICM does not consider skill. ICM determines equities based on a random progression of the tournament, but a skilled player can surely do better than that. Even when the average stack is only 10 BBs, skill still matters.
- ICM does not consider chip utility. Player 1 can use his big stack to bully Player 4, who may be waiting for Player 5 to bust out. Player 1's stack is worth more than an ICM model would predict, even if the players are equally skilled.
- ICM does not consider table position. (Is the big stack on my left?)
- ICM doesn't consider where we next post the blinds/antes or when they will be increased. In fact, ICM doesn't know the blinds even exist.
So What Should We Do?
Clearly the "fairest" method for everyone is to use the ICM method for chopping. By "fair" I mean that ICM is reasonable and consistent over a wide range of circumstances.
If I am the big stack and someone suggests an equal chop, I would refuse; it just doesn't give me enough of the prize pool. If they suggest a chip-chop, it would be to my advantage to agree. (Though I think this is ethically challenged.)
If I am the small stack and an equal chop is suggested, it would be to my advantage to agree. But a chip-chop would not be good for me; I would make more with an ICM chop.
If I am the most skilled player, I might suggest an extra bump. But would everyone agree to that? If I am clearly the most-skilled player, my best option might be to simply keep playing. Nevertheless, chopping reduces the variance that inevitably results from short-stacked play. And it saves time, which might come into play when fatigue is a factor in the quality of our play.
Conclusion
ICM is clearly the fairest chopping method we can choose. The "error" of the other methods will depend on the disparity among the stack sizes. If all of the stacks are nearly the same, then an equal chop will not be especially unfair. But there is no real need to be lazy about it. Any tournament director that allows a chop will have an ICM calculator, so all we need do is to agree on an ICM chop, sit back, and collect our prizes.
Steve Selbrede is the author of six poker books: The Statistics of Poker, Beat the Donks, Donkey Poker Volume 1: Preflop, Donkey Poker Volume 2: Postflop, Donkey Poker Volume 3: Hand Reading, and Tournament Poker for the Rest of Us.









